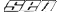The Laplace Transformation is the integral from 0 to infinity of ( e^-(s)t )( f(t) ), which as you mentioned gives you a function F(s)
Take the simplest example where f(t) = 1
I will use the notation "0|infinity" as "the integral from 0 to infinity"
L{1} = 0|infinity e^-st dt
=lim_A->infinity [ -(1/s)e^-s(A) - (-((1/s)e^-s(0)) ]
= 1/s
So for f(t) = 1, F(s) = L{1} = 1/s
(likewise L{n} = n/s)
The next simplest example is L{e^at}
= 0|infinity ( (e^-st)(e^at) )dt
= 0|infinity (e^-(s-a)t)dt
which evaluates to
F(s) = 1/(s-a)
For numerous functions f(t) we can build a table of F(s)'s, much like the table of integrals in the back of a calculus book.
If we have the function in some F(s) form, we can use L^-1{F(s)} to get f(t)
These operations become very useful in the analysis of differential equations
Take y'' - 2y' + y = cosine(t)
If we take the Laplace transform of the function it becomes (and Laplace transforms are linear so you can move the two out of the curly brackets)
L{y''} + 2L{y'} + L{y} = L{cos(t)}
Another useful property of the L{ } is that L{y'} is directly related to L{y} ( didn't derive it here, but these are the equ's)
L{y'} = sL{y} - y(0)
L{y''} = (s^2)L{y} - sy(0) - y'(0)
If we take the initial condition of y and y prime to be 0 to simplify things, and we substitute in for L{y'} and L{y''} we get
(s^2)L{y} + 2sL{y} + L{y} = L{cos(t)}
From a table of F(s)'s we know that L{cos(t)} = (s^2)/[(s^2) + (1^2)] (I write 1^2 because the coefficient of the t in cos(t) is 1)
so we have
(s^2)L{y} + 2sL{y} + L{y} = (s^2)/[(s^2) + (1^2)]
(s^2 + 2s +1)L{y} = (s^2)/[(s^2) + (1^2)]
(s+1)(s+1)L{y} = (s^2)/[(s^2) + (1^2)]
L{y} = (s^2)/[(s^2) + (1^2)][(s+1)(s+1)]
If we use partial fractions to separate the big 's' expression into smaller parts, we end up with expressions like 1/(s-a), which we know from our table is the L^-1{e^at}. After solving the L^-1{y} on both sides, we are left with y, which is the solution to our differential equation.
None.